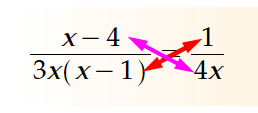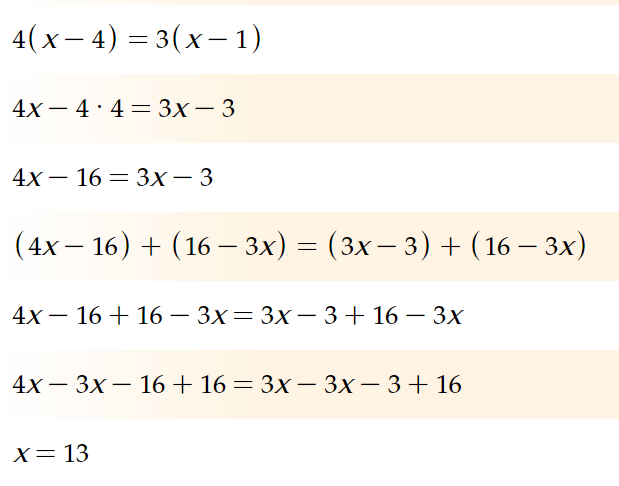The problem
Hi, can you please more in detail how to apply the distributive property in this problem? I don’t understand how and when to apply the property?
x-4/
3x(x-1)
=
1/
4x
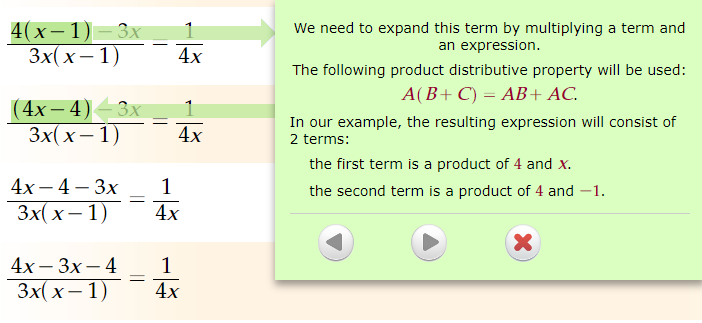
We need to expand this term by multiplying a term and an expression.
The following product distributive property will be used:
A(B+ C) = AB + AC.
In our example, the resulting expression will consist of 2 terms:
the first term is a product of 4 and
X. the second term is a product of 4
and -4.
4x -4•4 = 3x- 3
4x - 16 = 3х - 3
Answer provided by our tutors
Distributive property says "A*(B + C) = A*B + A*C".
This propety is applied when multiplying:
4*(x - 1)
So, A = 4, B = x and C = -1, if we replace the values we get:
4*(x - 1) = 4*x - 4*1 = 4x - 1
Next, the operations in the denominator and numerator are perfromed and then we want to get rid of the fraction.
We can do that by cross-multiplying