The problem
I need help with This,
"Find a quadratic equation with x-intercepts -3 and 2 and a y-intercept of 12. Put it in standard form" I don't know how to use your site to get the answer.
thank you
Answer provided by our tutors
The standard form of quadratic equation is:
'y = ax^2+bx+c',
where 'a', 'b' and 'c' are constants and 'x' and 'y' are variables.
From the text of the problem we know that the line goes trough (-3, 0),(2, 0) and (0, 12).
This means that we can plug the values for 'x' and 'y' to find 'a', 'b' and 'c'.
For (x, y) = (-3, 0) we have:
a(-3)^2 + b*(-3) + c = 0
9a - 3b + c = 0
For (x, y) = (2, 0) we have:
a(2)^2 + b*2 + c = 0
4a + 2b + c = 0
For (x, y) = (0, 12) we have:
a*0^2 + b*0 + c = 12
c = 12
If we plug c = 12 into '9a - 3b + c = 0' and '4a + 2b + c = 0' we get a system of equations:
9a - 3b + 12 = 0
4a + 2b + 12 = 0
......
Click here to see the system of equations solved for a and b
'
a = -2
b = -2
The standard form of quadratic equation is:
y = -2x^2 - 2x + 12
If we graph the equation we see that the line indeed goes trough the -3, 0),(2, 0) and (0, 12):
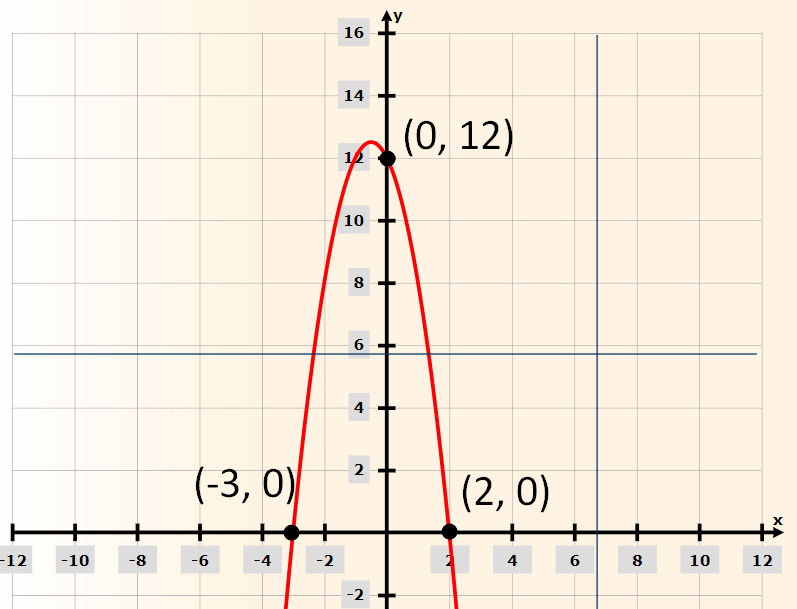
Click here is you want to see the graph.
