The problem
Click to see the original problem
In the problem 2(x+y)^2+(x+y)-6, the steps show that I have to go from 2x^2+4xy+2y^2+x+y-6 to (y+x+2)(2y+2x-3). There is no explanation for this step. How did you transition between these steps?
Answer provided by our tutors
2(x+y)^2+(x+y)-6 =
= 2(x+y)^2 + (-3(x+y) + 4(x+y))-6 =
= 2(x+y)^2-3(x+y) + 4(x+y)-6 =
= (x+y)(2(x+y)-3) + 2(2(x+y)-3) =
= (2(x+y)-3)(x+y+2)=
= (2x+2y-3)(x+y+2)
Another way to factor the above expression is to substitute 'x+y' with 't' (that is 't = x+y') and to factor 2t^2+t-6:
click here to see the step by step factorization
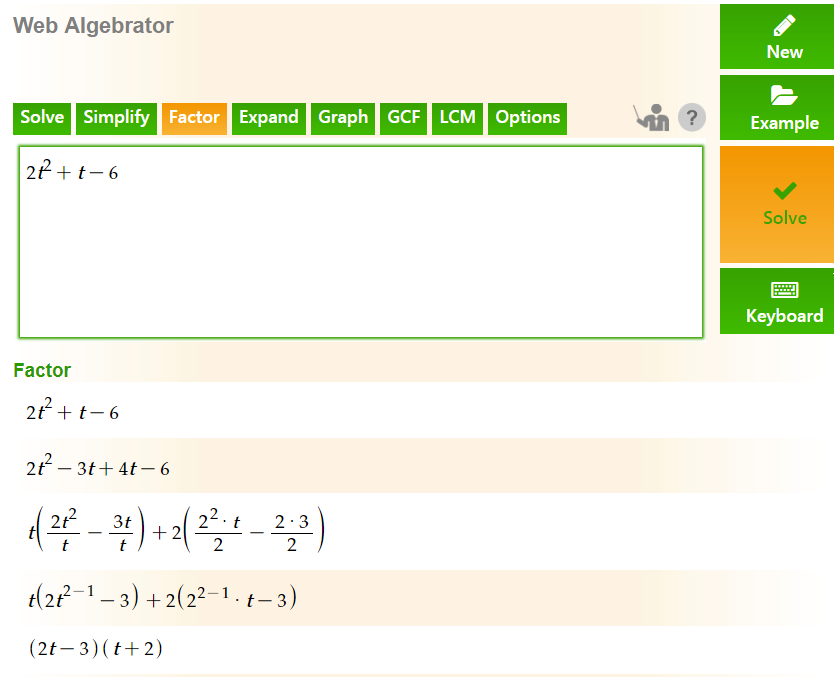
And than plug 'x+y' instead of 't' and you'll get:
(2(x+y)-3)(x+y+2)
